°°°°Ķŕ∂ĢĻĚ(ji®¶)°°ňéőÔīķ÷xĄ”(d®įng)ѶĆW(xu®¶)ÖĘĒĶ(sh®ī)ľį∆šĎ™(y®©ng)”√
°°°°ěťŃň∂®ŃŅĶō√Ť ŲůwÉ»(n®®i)ňéŃŅŽSēr(sh®™)ťg◊ÉĽĮĶń“é(gu®©)¬…–‘���£¨≥£ĹŤ÷ķĒĶ(sh®ī)ĆW(xu®¶)Ķń‘≠ņŪļÕ∑Ĺ∑®ĀŪ(l®Ęi)ÍU√ų���°£
°°°°“Ľ��°ĘňéőÔĶńēr(sh®™)ŃŅÍP(gu®°n)ŌĶļÕēr(sh®™)–ßÍP(gu®°n)ŌĶ
°°°°ēr(sh®™)ŃŅÍP(gu®°n)ŌĶ:—™Ě{ňéőÔĚ‚∂»ŽSēr(sh®™)ťgĶńÕ∆“∆∂Ýįl(f®°)…ķ◊ÉĽĮĶń“é(gu®©)¬…�����°£
°°°°”√ēr(sh®™)ŃŅ«ķĺÄĪŪ ĺ£ļĹoňéļů�����£¨≤ĽÕ¨ēr(sh®™)ťg≤…ľĮ—™ė”����£¨∑÷»°—™Ě{��£¨”√ŖmģĒ(d®°ng)?sh®ī)ń∑Ĺ∑®úy(c®®)∂®—™Ě{÷–ĶńňéőÔĚ‚∂»�����£¨“‘ēr(sh®™)ťgěťôM◊Ýėň(bi®°o)����°Ę—™ňéĚ‚∂»ěťŅv◊Ýėň(bi®°o)£¨Ķ√ĶĹ∑ī”≥—™Ě{÷–ňéőÔĚ‚∂»Ą”(d®įng)ĎB(t®§i)◊ÉĽĮĶń«ķĺÄ��£¨∑Q∆šěť—™ňéĚ‚∂»-ēr(sh®™)ťg«ķĺÄ�����£¨ľīēr(sh®™)ŃŅ«ķĺÄ�°£
°°°°—™ňéĚ‚∂»◊ÉĽĮ°ķ∑ī”≥◊ų”√≤ŅőĽňéőÔĚ‚∂»Ķń◊ÉĽĮ°ķňéőÔĶń–ßĎ™(y®©ng)ŽSēr(sh®™)ťg◊ÉĽĮ°£
°°°°ĪŪ¨F(xi®§n)£ļňé–ߏńÔ@–ßĶĹŌŻ ßĶńŖ^(gu®į)≥Ő���£¨ňé–ßŇcēr(sh®™)ťgĶńŖ@∑NÍP(gu®°n)ŌĶ≥…ěťňéőÔĶńēr(sh®™)–ßÍP(gu®°n)ŌĶ�����°£
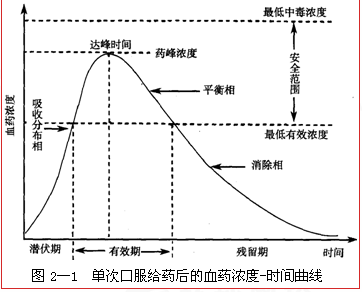
°°°°ąD2°™1ěťÜőīőŅŕ∑ĢĹoňéļů—™ňéĚ‚∂»-ēr(sh®™)ťg«ķĺÄ��£¨∑ī”≥ňéőÔőŁ ’��°Ę∑÷≤ľļÕŌŻ≥ż÷ģťgĶńŌŗĽ•ŌŻťL(zh®£ng)ĶńÍP(gu®°n)ŌĶ�����°£
°°°°«ķĺÄ∑÷ěť»żŌŗ£ļ
°°°°őŁ ’∑÷≤ľŌŗ£ļ«ķĺÄĶń…Ō…ż∂ő�����£¨ňéőÔ◊‘Ĺoňé≤ŅőĽ—łňŔőŁ ’�£¨—łňŔŌÚĹMŅó÷–∑÷≤ľ£¨ňéőÔőŁ ’Ŗh(yu®£n)īů”ŕŌŻ≥ż��°£
°°°°∆Ĺļ‚Ōŗ£ļ«ķĺÄĶń÷–ťg∂ő�£¨ňéőÔőŁ ’ňŔ¬ ļÕŌŻ≥żňŔ¬ ŌŗģĒ(d®°ng)£¨ůwÉ»(n®®i)ňéŃŅŖ_(d®Ę)ĶĹēļēr(sh®™)ĶńĄ”(d®įng)ĎB(t®§i)∆Ĺļ‚����£¨—™ňéĚ‚∂»Ķń◊ÉĽĮŕÖ”ŕ∆Ĺ台£
°°°°ŌŻ≥żŌŗ£ļ«ķĺÄĶńŌ¬ĹĶ∂ő�£¨—™ňéĚ‚∂»—łňŔŌ¬ĹĶ°£
°°°°«ķĺÄŌ¬√ś∑e(AUC)£ļēr(sh®™)-ŃŅ«ķĺÄŌ¬ňýł≤…wĶń√ś∑e���£¨∑ī”≥ňéőÔ‘ŕ—™“ļ÷–ĶńŅāŃŅ�����°£“‚Ńx£ļ∑ī”≥ňéőÔĶńőŁ ’≥Ő∂»��£¨Ć¶(du®¨)”ŕÕ¨“Ľ ‹‘á’Ŗ£¨AUCīůĄtňéőÔőŁ ’≥Ő∂»łŖ�����°£
°°°°«ķĺÄ”÷Ņ…∑÷ěť»ż∆ŕ£ļ
°°°°Ěď∑Ł∆ŕ£ļĹoňéļůĶĹť_(k®°i) ľ≥Ų¨F(xi®§n)Įü–ßĶńēr(sh®™)ťg°£∑ī”≥ňéőÔĶńőŁ ’Ňc∑÷≤ľ�£¨“≤ŇcňéőÔĶńŌŻ≥ż”–ÍP(gu®°n)°£
°°°°”––ß∆ŕ£ļňéőÔĺS≥÷‘ŕ◊ÓĶÕ”––ßĚ‚∂»÷ģ…ŌĶńēr(sh®™)ťg�����°£ťL(zh®£ng)∂Ő»°õQ”ŕňéőÔĶńőŁ ’ļÕŌŻ≥żňŔ¬ ���°£
°°°°‘ŕīň∆ŕ÷–£ļ
°°°°—™ňéĚ‚∂»”–“Ľ∑Ś÷Ķ�����£¨∑Qěť∑ŚĚ‚∂»���°£Ć¶(du®¨)”ŕŐō∂®ĶńňéőÔ÷∆Ą©£¨∑ŚĚ‚∂»ŇcĹoň饩ŃŅ≥…’żĪ»����°£
°°°°Ŗ_(d®Ę)ĶĹ∑ŚĚ‚∂»ňý–ŤĶńēr(sh®™)ťg∑QěťŖ_(d®Ę)∑Śēr(sh®™)ťg£¨∆šťL(zh®£ng)∂ŐŇcőŁ ’ļÕŌŻ≥żĶńňŔ¬ ”–ÍP(gu®°n)�����°£
°°°°C maxļÕTmaxĶńīů–°ĺCļŌ∑ī”≥ňéőÔ÷∆Ą©ĶńőŁ ’�����°Ę∑÷≤ľ°ĘŇŇ–ĻļÕīķ÷x«ťõr���°£Õ¨“Ľ ‹‘á’ŖCmaxļÕTmax÷ų“™ŇcňéőÔ÷∆Ą©”–ÍP(gu®°n)�����°£
°°°°öąŃŰ∆ŕ£ļ—™ňéĚ‚∂»“—ĹĶĶĹ◊ÓĶÕ”––ßĚ‚∂»“‘Ō¬����£¨÷Ī÷ŃÕÍ»ęŹńůwÉ»(n®®i)ŌŻ≥żĶńēr(sh®™)ťg�����°£ťL(zh®£ng)∂Ő»°õQ”ŕňéőÔĶńŌŻ≥żňŔ¬ �°£ňĮ√ŖňéőÔöąŃŰ∆ŕťL(zh®£ng)‘ŕůwÉ»(n®®i)”––Ó∑e¨F(xi®§n)Ōů£¨∑īŹÕ(f®ī)”√ňé“◊÷¬–Ó∑e÷–∂ĺ���°£
°°°°∂Ģ����°Ę∑Ņ “ń£–Õ
°°°°∑Ņ “ń£–Õ(compartment model)£ļŹńňŔ∂»’ďĶńĹ«∂»≥Ųįl(f®°)£¨Ĺ®ŃĘ“ĽāÄ(g®®)ĒĶ(sh®ī)ĆW(xu®¶)ń£–ÕĀŪ(l®Ęi)ń£ĒMôC(j®©)ůw�����°£ĆĘ’ŻāÄ(g®®)ôC(j®©)ůw“ēěť“ĽāÄ(g®®)ŌĶĹy(t®Įng)�£¨‘ŔĆĘ‘ďŌĶĹy(t®Įng)įīĄ”(d®įng)ѶĆW(xu®¶)ŐōŁc(di®£n)∑÷읻۳…āÄ(g®®)∑Ņ “�°£
°°°°∑Ņ “£ļ
°°°°(1)≥ťŌůłŇńÓ£¨ĆĘňéőÔřD(zhu®£n)Ŗ\(y®īn)ňŔ¬ ŌŗĹŁĶńĹMŅó∆ųĻŔöwľ{ěť“ĽāÄ(g®®)∑Ņ “���°£≤ĽīķĪŪń≥āÄ(g®®)ĺŖůwĶńĹ‚∆ ĆW(xu®¶)…ŌĶńĹMŅó∆ųĻŔ��°£
°°°°(2)Õ¨“ĽāÄ(g®®)∑Ņ “÷–��£¨łųĹMŅó≤ŅőĽĶńňéŃŅ≤Ľ“Ľ∂®ŌŗĶ»��£¨‘ŕ∆šťgĶńřD(zhu®£n)Ŗ\(y®īn)ňŔ¬ «Ōŗň∆Ķń�°£
°°°°ňéőÔ‘ŕůwÉ»(n®®i)ĶńřD(zhu®£n)Ŗ\(y®īn)ļÕŌŻ≥ż��£¨įī“ĽľČ(j®™)Ŗ^(gu®į)≥ŐŖM(j®¨n)––���£¨“Úīň�����£¨”÷∑QěťĺÄ–‘∑Ņ “ń£–Õ�����£¨∆šĄ”(d®įng)ѶĆW(xu®¶)Ŗ^(gu®į)≥ŐěťĺÄ–‘Ą”(d®įng)ѶĆW(xu®¶)����°£
°°°°≥£“ä(ji®§n)Ķń∑Ņ “ń£–Õ”–£ļ“Ľ “ń£–ÕļÕ∂Ģ “ń£–ÕĶ»°£
°°°°1.“Ľ “ń£–Õ
°°°°“Ľ “ń£–Õ£ļľŔ∂®…Ūůw”…“ĽāÄ(g®®)∑Ņ “ĹM≥…���£¨žo√}◊Ę…šĹoňéļů�����£¨ňéőÔń‹ŅžňŔ∑÷≤ľĶĹ»ę…ŪĶńůw“ļļÕĹMŅó÷–��£¨—™Ě{÷–ňéőÔĚ‚∂»ŇcĹMŅó÷–ňéőÔĚ‚∂»ŅžňŔŖ_(d®Ę)ĶĹĄ”(d®įng)ĎB(t®§i)∆Ĺļ‚���°£
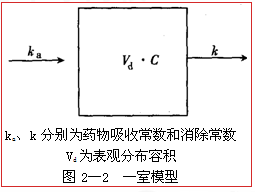
°°°°žo√}◊Ę…šĹoňé£ļ—™ňéĚ‚∂»C(ƶ(du®¨)ĒĶ(sh®ī)Ě‚∂»)-ēr(sh®™)ťgt«ķĺÄěťÜő÷łĒĶ(sh®ī)ļĮĒĶ(sh®ī)°£
°°°°”č(j®¨)ň„ Ĺ£ļ
°°°°C=D/V°§e -kt=C0°§e-kt
°°°°C“Ľ∂őēr(sh®™)ťgļůĶń—™ňéĚ‚∂»�£¨C oěť≥ű ľ—™ňéĚ‚∂»£¨◊Ę…šĄ©ŃŅěťD����£¨V∑÷≤ľ»›∑e=D/C0�£¨tēr(sh®™)ťg����£¨kŌŻ≥żňŔ¬ ≥£ĒĶ(sh®ī)£¨e◊‘»ĽĆ¶(du®¨)ĒĶ(sh®ī)÷ģĶ◊ĒĶ(sh®ī)ěť2.718�����°£
°°°°ĆĘC=C o°§e-ktłńĆĎ(xi®ß)ěť£ļln(C/Co)=-kt�°£
°°°°lnCƶ(du®¨)ēr(sh®™)ťgt◊ųąD���£¨Ķ√ĶĹ“Ľól÷ĪĺÄ�����£¨–Ī¬ ěťk o
°°°°įīÜő “ń£–ÕŐé÷√ĶńňéőÔ��£¨žo◊ĘĹoňéļů�����£¨—™ňéĚ‚∂»(ƶ(du®¨)ĒĶ(sh®ī)Ě‚∂»)-ēr(sh®™)ťg«ķĺÄ≥ ÷ĪĺÄÍP(gu®°n)ŌĶ��°£
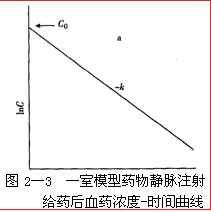
°°°°“Ú?y®§n)ť£ļ—™ňéĚ‚∂»Ō¬ĹĶ“ĽįŽňý–ŤĶńēr(sh®™)ťg∑QěťįŽň•∆ŕ(t 1/2)���£¨C=0.5Coēr(sh®™)����£¨Ķ√ĶĹt1/2=ln0.5/(-k)=0.693/k�����°��£Ņ…“ä(ji®§n)įŽň•∆ŕŇcŌŻ≥żňŔ¬ ≥£ĒĶ(sh®ī)≥…∑īĪ»����°£
°°°°ŌŗÍP(gu®°n)Õ∆ň]£ļ
2010ąŐ(zh®™)ėI(y®®)ňééüňé ¬Ļ‹ņŪŇc∑®“é(gu®©)ń£ĒMÓ}ľįīūįłÖRŅā









